Convergence of the gamma function

April 26, 2012

I will write up the proof of the convergence of the gamma function as a follow-up to this post, where I show why the exponential grows faster than any polynomial. The gamma function is defined by

$\Gamma(s) = \displaystyle\int_{0}^{\infty} e^{-t}t^{s-1}dt.$

Proposition: This integral converges for $s > 0.$

Proof: Let’s divide the integral in a sum of two terms,

$\Gamma(s) = \displaystyle\int_0^1 e^{-t}t^{s-1}dt + \int_1^{\infty}e^{-t}t^{s-1}dt.$

For the first term, since the function $e^{-t}$ is decreasing, it’s maximum on the interval $[0,1]$ is attained at $t = 0$ so

$\displaystyle\int_0^1 e^{-t}t^{s-1}dt < \int_0^1t^{s-1}dt.$

But for $s > 0,$ this last integral converges to $1/s.$

For the second term, we use what we showed in this post: since the exponential grows faster than any polynomial, for every $s$ we can take $N \in \textbf{N}$ so big that $t \geq N \Rightarrow e^{t/2} > t^{s-1}.$ So

$\displaystyle\int_1^{\infty}e^{-t}t^{s-1}dt = \int_1^Ne^{-t}t^{s-1}dt + \int_N^{\infty}e^{-t}t^{s-1}dt$

$< \displaystyle\int_1^Ne^{-t}t^{s-1}dt + \int_N^{\infty} e^{-t}e^{t/2}dt$

$= \displaystyle\int_1^Ne^{-t}t^{s-1}dt + \int_N^{\infty}e^{-t/2}dt$

$< \infty$

which completes the proof.

From → Analysis, Real Analysis

3 Comments

Erica Liu permalink

May I ask why e^(t/2) was chosen not e^(t/3) for instance for the second term? Much appreciated.

Reply
Madeline permalink

I don’t think it makes a difference what is used (e^(t/2) or something else) so long as it is in fact > x^(p-1). For instance what if we used e^x? e^x > x^(p-1). Using e^x would make it even more obvious.

Reply
- J-F Arbour permalink
  
  It is true that we could also use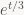 $e^{t/3}$ because it’s greater than $t^{s-1}$ for any $s$ , but also because $e^{-t}e^{t/3}$ is integrable. What you suggest Madeline doesn’t work, if we take $e^t$ instead of $e^{t/2}$ , then we get $\int_N^{\infty}e^{-t}t^{s-1} < \int_N^{\infty}e^{-t}e^{t} = \int_N^{\infty}1 = +\infty$ and we can’t conclude anything.
  
  Reply